SUDOKU
Les règles du sudoku
La grille de sudoku est composée de 9 x 9 carrés, divisée en 9 sous-grilles bornées de grosses lignes. Certains carrés contiennent déjà un chiffre de 1 à 9. Le but de jeu, c’est de remplir les carrés vides avec les chiffres de 1 à 9 en observant les règles suivantes.- Chaque ligne du sudoku, on la remplit avec les chiffres de 1 à 9. Chaque chiffre ne se trouve jamais plus qu’une fois sur la même ligne.
- Chaque colonne du sudoku, on la remplit avec les chiffres de 1 à 9. Chaque chiffre ne se trouve jamais plus qu’une fois sur la même colonne.
- Dans chaque sous-grille du sudoku, on la remplit avec les chiffres de 1 à 9. Chaque chiffre ne se trouve jamais plus qu’une fois dans la même sous-grille.
Sudoku pour tout le monde
Nous avons preparé les jeux des niveaux différents pour que les débutants, les avancés et même les experts du sudoku tous puissent trouver un jeu pour eux.- Sudoku facile
- convenable à ceux qui sont encore les débutants ou ceux qui ne veulent pas se pressurer le cerveaux.
- Sudoku intermédiaire
- convenable aux avancés
- Sudoku difficile
- pour tout le monde qui aime faire travailler sa matière grise
- Sudoku très difficile
- seulement les vrais experts reusirront à résoudre ces jeux de sudoku
Comment jouer au sudoku
On montre quelques méthodes pour aider ceux qui encore apprennent à faire ce type de casse-tête. Il y a des jeux simples aussi que des jeux plus difficiles.
Un seul candidat
La technique la plus simple et utilisée le plus souvent pour résoudre un sudoku. On décide quel chiffre peut être rempli dans un carré. On utilise la méthode d’elimination. On décide quels chiffres ne peuvent pas être utilisés parce qu’ils se trouvent déja sur la même ligne, la même colonne ou la même sous-grille. S’il y a seulement un seul chiffre possible qui peut se trouver dans le carré, on peut l‘écrire.
On montrera cette méthode à l’aide de l’exemple suivant. On cherchera les chiffres qui conviennent pour le premier carré et la première ligne.
chiffre 1 - ne convient pas, il se trouve déjà dans la ligne et aussi dans la colonne; chiffre 2 - ne convient pas, il se trouve déjà dans la ligne et aussi dans la sous-grille; chiffre 3 - ne convient pas, il se trouve déjà dans la sous-grille chiffre 4 - ne convient pas, il se trouve déjà dans la ligne; chiffre 5 - ne convient pas, il se trouve déjà dans la colonne; chiffre 6 - ne convient pas, il se trouve déjà dans la sous-grille; chiffre 7 - ne convient pas, il se trouve déjà dans la ligne et aussi dans la sous-grille; chiffre 8 - convient;, chiffre 9 - ne convient pas, il se trouve déjà dans la ligne
Donc, il nous reste une seule possibilité – le chiffre qui se trouvera dans le premier carré, cela sera le chiffre 8.

Candidat unique
Si on ne trouve aucun autre chiffre en utilisant la méthode précédente, cet algorithme est souvent utile. En suivant la méthode d’une seule position possible, on cherche un carré ou on peut mettre le chiffre donné.
On montrera cette méthode à l’aide de l’exemple. On cherchera une position dans la première sous-grille pour le chiffre 1.

On peut appliquer la même méthode en cherchant une selue position possible pour un chiffre dans la ligne ou dans la colonne.
En utilisant ces deux méthodes, on peut résoudre un grand nombre de puzzles. Sur notre site, il est possible de résoudre tous les sudokus de niveau facile avec ces méthodes.
Les méthodes avec plusieurs carrés en même temps
Utilisant les algorithmes précédents, nous avons cherché toujours un chiffre pour un seul carré, ou bien nous avons cherché un carré pour un seul chiffre. Mais tous les puzzles ne peuvent pas être résolues par ces deux méthodes uniquement. Quelquefois, il faut considérer plusieurs carrés en même temps.
On montrera cette méthode encore à l’aide de l’exemple. On déterminera les positions pour les chiffres dans la première sous-grille.
Dans la première sous-grille, on manque les chiffres 3, 7 et 8. Le chiffre 3 peut se trouver dans tous les carrés. Le chiffre 7 ne peut pas se trouver dans la première ligne, parce qu’il s’y trouve déjà. Donc, il peut être dans le carré jaune ou vert. Pareillement, le chiffre 8 peut se trouver seulement dans le carré vert ou jaune. Le carré jaune et le carré vert, ils seront occupés par les chiffres 7 et 8. Nous ne savons pas déjà la position exacte de tous les deux chiffres, mais il est sûr qu’ils occuperont les deux carrés. Alors, le chiffre 3 ne peut pas se trouver dans le carré jaune ni dans le carré vert parce qu’il n’y aurait pas un carré pour le chiffre 7 ou le chiffre 8. Donc, il nous reste une seule position pour le chiffre 3, c’est le carré blanc.
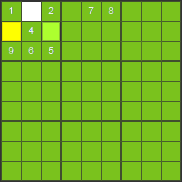
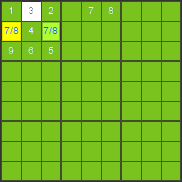
Nous avons montré un exemple facile pour illustrer la situation quand il faut considérer plusieurs carrés en même temps. On peut appliquer la même méthode en considérant les lignes ou les colonnes.
Les méthodes essais-erreurs
Si tous les méthodes sont sans résultat, il n’y a qu’une seule possibilité à résoudre le sudoku. Il faut deviner la valeur dans un carré et si on aboutit un résultat fautif, il faut se retourner à travers le processus jusqu’à la valeur devinée. Si on devine, il est convenable de deviner la valeur de tel carré où il y a moins possibilités ou deviner la valeur, qui nous semble improbable pour qu’on atteigne un état d’erreur.
Sur ce site, utiliser cette méthode n’est nécessaire qu’en résolvant les sudokus les plus difficiles.
 Après avoir eliminé toutes les possibilités sauf 8 il est évident que le chiffre 8 se trouvera dans le premier carré de la première colonne.
Après avoir eliminé toutes les possibilités sauf 8 il est évident que le chiffre 8 se trouvera dans le premier carré de la première colonne.
 On elimine les positions où le chiffre 1 ne peut pas se trouver.
On elimine les positions où le chiffre 1 ne peut pas se trouver.
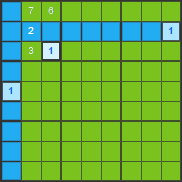 Il nous reste une seule position pour le chiffre 1 – c’est dans la troisième ligne et la troisième colonne.
Il nous reste une seule position pour le chiffre 1 – c’est dans la troisième ligne et la troisième colonne.
 Il nous reste une seule position pour le chiffre 3, c’est le carré blanc. On le peut écrire là.
Il nous reste une seule position pour le chiffre 3, c’est le carré blanc. On le peut écrire là.